树
平衡二叉树
定义
我们知道,在利用树形查找时,树的高度会影响查找的效率。因此,在构建树的过程中,为了避免树的高度增长过快,降低二叉排序树的性能,我们通常会要求任意节点的左右子树高度之差(绝对值)不超过1。这样的树便被称为平衡二叉树,又名AVL树。
注意:平衡二叉树是特殊的二叉排序树!
平衡因子
左右子树高度之差,我们便称之为平衡因子,平衡二叉树的平衡因子只可能为-1 , 0 , 1。
如何区分平衡与不平衡?
下面是一组平衡二叉树和非平衡二叉树的对比图:
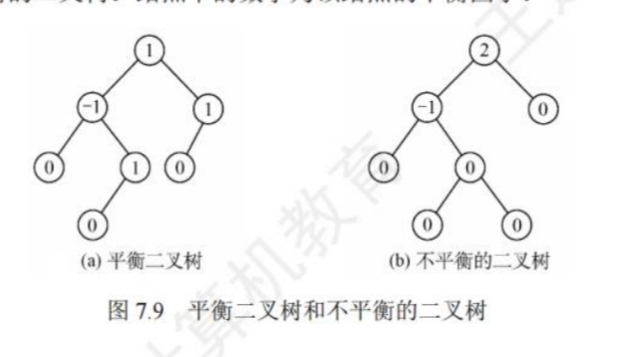
在上图的非平衡二叉树中,节点2的左子树高度为3,右子树的高度为1,两边子树高度只差(平衡因子)的绝对值为2,超过了最大值1,因此这是一颗不平衡子树。而左边的平衡二叉树中的所有节点的平衡因子都不超过1。
平衡二叉树的插入
那么了解了AVL树的定义后,我们都能联想到一个问题:如果对AVL树进行插入操作的话,那是不是很有可能会破坏树的平衡状态?例如我在上图中的平衡二叉树中的第四层的叶子节点0下再插入一个节点,那么这棵树的平衡状态就会被破坏了,因为节点-1的左子树高度为1,而右子树的高度为3,平衡因子显然大于1。
那么有什么办法能够既能够插入数据,插入的数据不改变二叉排序树的性质,又不影响平衡二叉树的性质呢?很遗憾,是没有的。所以我们只能在插入数据后检查是否破坏了平衡性,若是不平衡的话则对最小不平衡树进行调整。(最小不平衡树:距离插入节点最近的,且平衡因子绝对值大于1的节点,以该节点为根节点构成的子树)。然而,在不同位置插入数据,所需要进行的调整也是不同的,调整的情况分为LL,LR,RL,RR。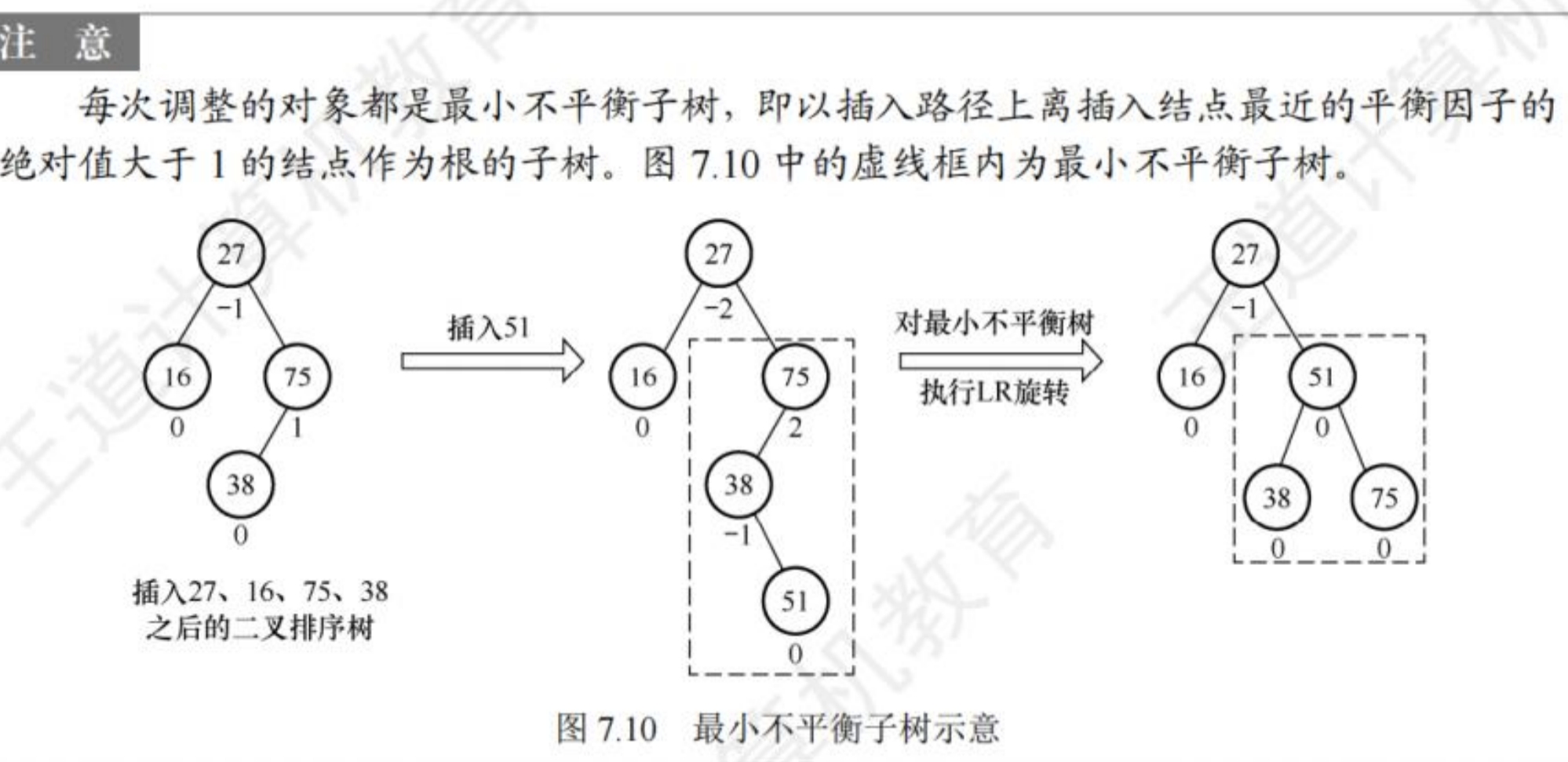
tips:接下来所说的”旋转”的操作可能会让人产生一些困惑或不解,我更倾向于将其理解为”替代”。尤其是在LR和RL中,他们的旋转操作可以理解为:带着他们的子树移动到某个位置。
LL旋转 (需要向右进行一次旋转)
在最小不平衡子树中,由于在节点A的左(L)孩子的左(L)子树上插入了新节点导致失去了平衡,因此需要进行一次向右的旋转操作。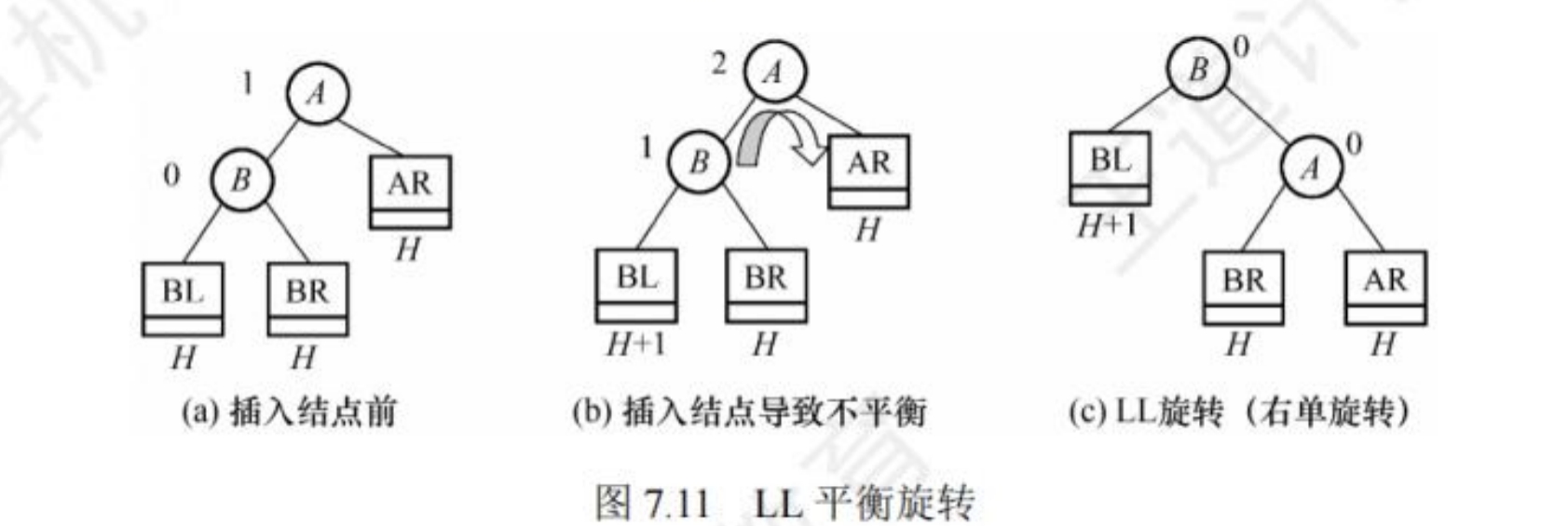
如图(节点旁的数字代表平衡因子):A的左孩子B向右上旋转代替A成为根节点,A向右下旋转成为B的右孩子,而B的原右子树则成为A的左子树。整个过程节点都是向右旋转,因此也叫做右旋。
这样调整的思路是,增高高度较小的一方子树,缩小高度较高的一方子树。如何缩小高度?通过增加节点的分支(由单分支变为双分支),再通过调整节点的位置使得其符合二叉排序树(左<根<右)的性质。
RR旋转(向左进行一次旋转)
在最小不平衡子树中,由于节点A的右(R)孩子的右(R)子树上插入了新节点,导致以A为根节点的子树失去平衡,需要一次向左的旋转操作。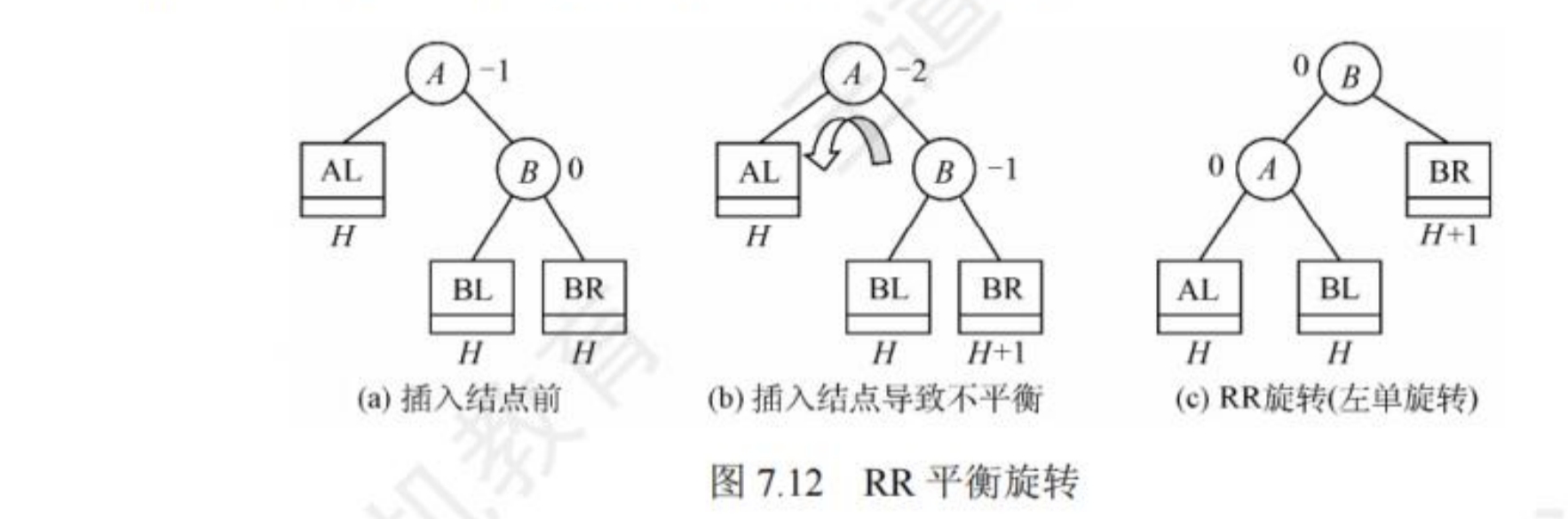
如图,将A的右孩子向左上旋转代替A成为根节点,将A向左下旋转成为B的左孩子,而B的原左子树则作为A的右子树。
LR旋转(向左进行一次旋转后向右进行一次旋转)
在最小不平衡子树中,由于节点A的左孩子(L)的右子树(R)插入了新的节点,导致以A节点为根的子树失去平衡,需要进行两次旋转操作,先向左旋转然后向右旋转。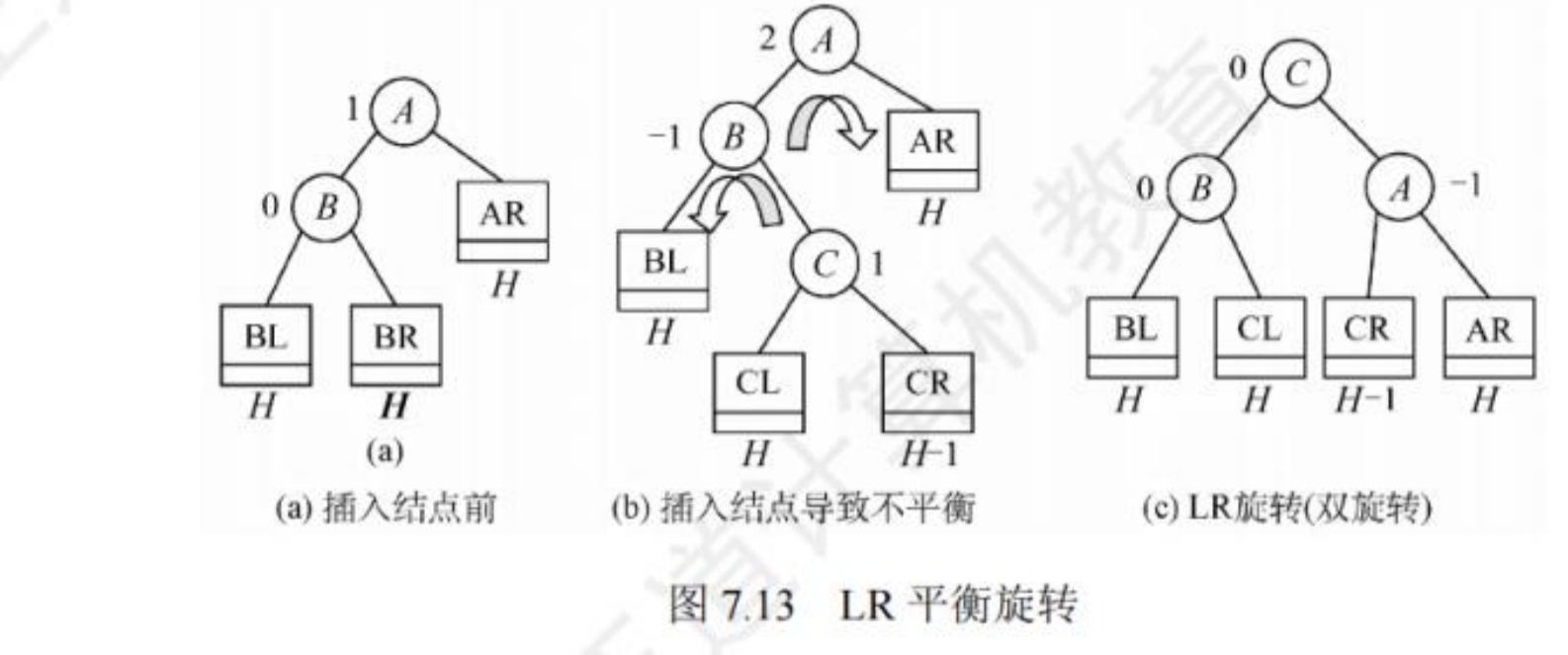
如图,先将A的左孩子B的右子树的根节点C向左上旋转至B的位置,然后把节点C向上旋转提升到A的位置。
RL旋转(先右旋后左旋)
在最小不平衡子树中,由于在A的右(R)孩子的左(L)子树上插入新的节点,导致以A节点为根的子树失去平衡,需要进行先右旋后左旋操作哦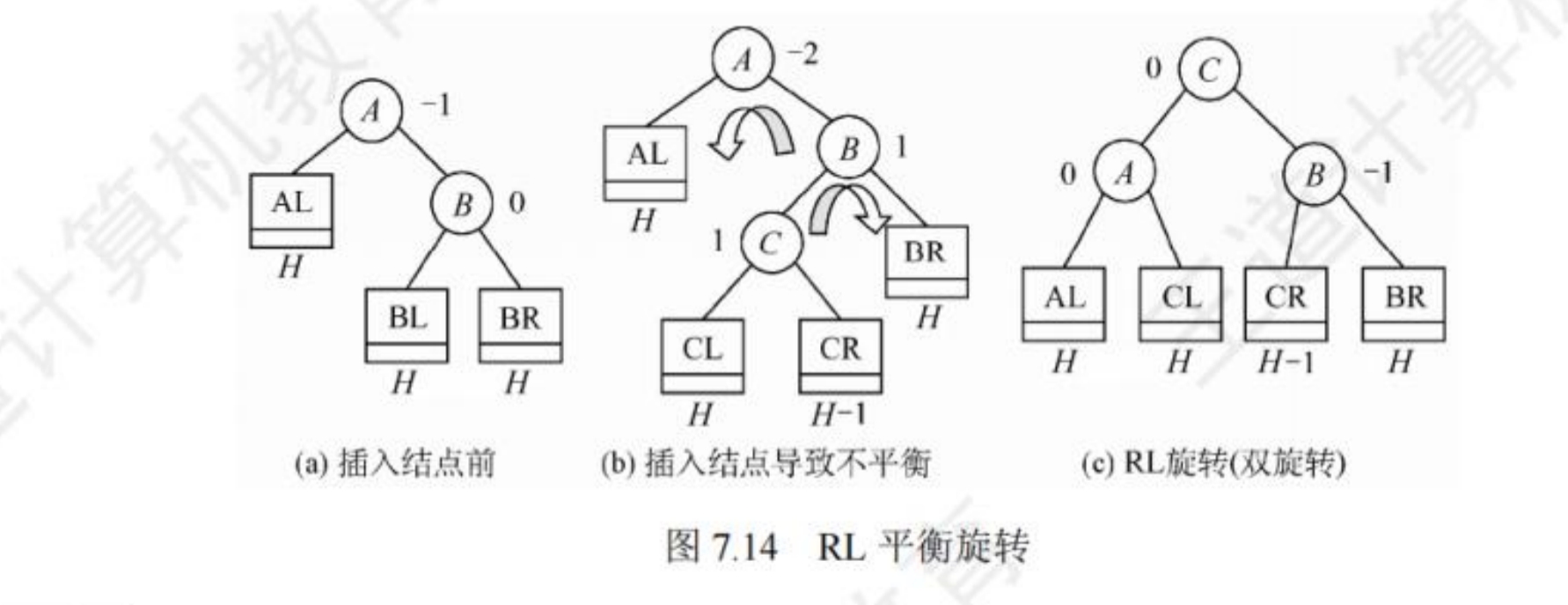
先将A的右孩子B的左子树的根节点C向右旋转上升到B的位置,然后把C向左上旋转上升到A的位置
如何记忆操作流程
总结的规律为:
(1)LL和RR的操作都是和字母反着来的,L的话就是右旋,R的话就是左旋
(2)LL和RR只需要重复的执行两次旋转操作就行,而LR和RL则是需要分别执行先左旋后右旋以及先右旋后左旋的操作
(3)先调整根节点的孩子,向上调整至根节点的位置。后调整根节点,向下调整至其孩子的位置。
(4)调整后,根节点A变为孩子节点,原根节点孩子方向上的子树调整为调整后的A的孩子,究竟是位于左孩子还是右孩子则取决于旋转时的方向(或根据二叉排序树:左<根<右的性质判断)。
如何构造平衡二叉树
构建平衡二叉树的过程和构建二叉排序树类似,根据插入元素的大小按照左<根<右的权重决定其插入的究竟是左孩子还是右孩子。
然而和构建二叉排序树不同的是,在构建平衡二叉树的时候还需要一个检测是否平衡的机制,如果说构造过程中新插入的节点导致了这棵树的平衡性遭到破坏的话,则需要按照上面那节:平衡二叉树的插入中的操作流程对二叉树进行一个调整。
以王道(2025数据结构)书中P298页中所举例子为例:在进行到步骤(d)时,新插入的节点7导致整棵树失衡,此时节点7是以节点15为根的最小不平衡子树的左孩子的右子树,属于情况:LR,因此需要进行先左旋后右旋的操作。在步骤(e)和步骤(g)时遇到的不平衡所应对的方法类似。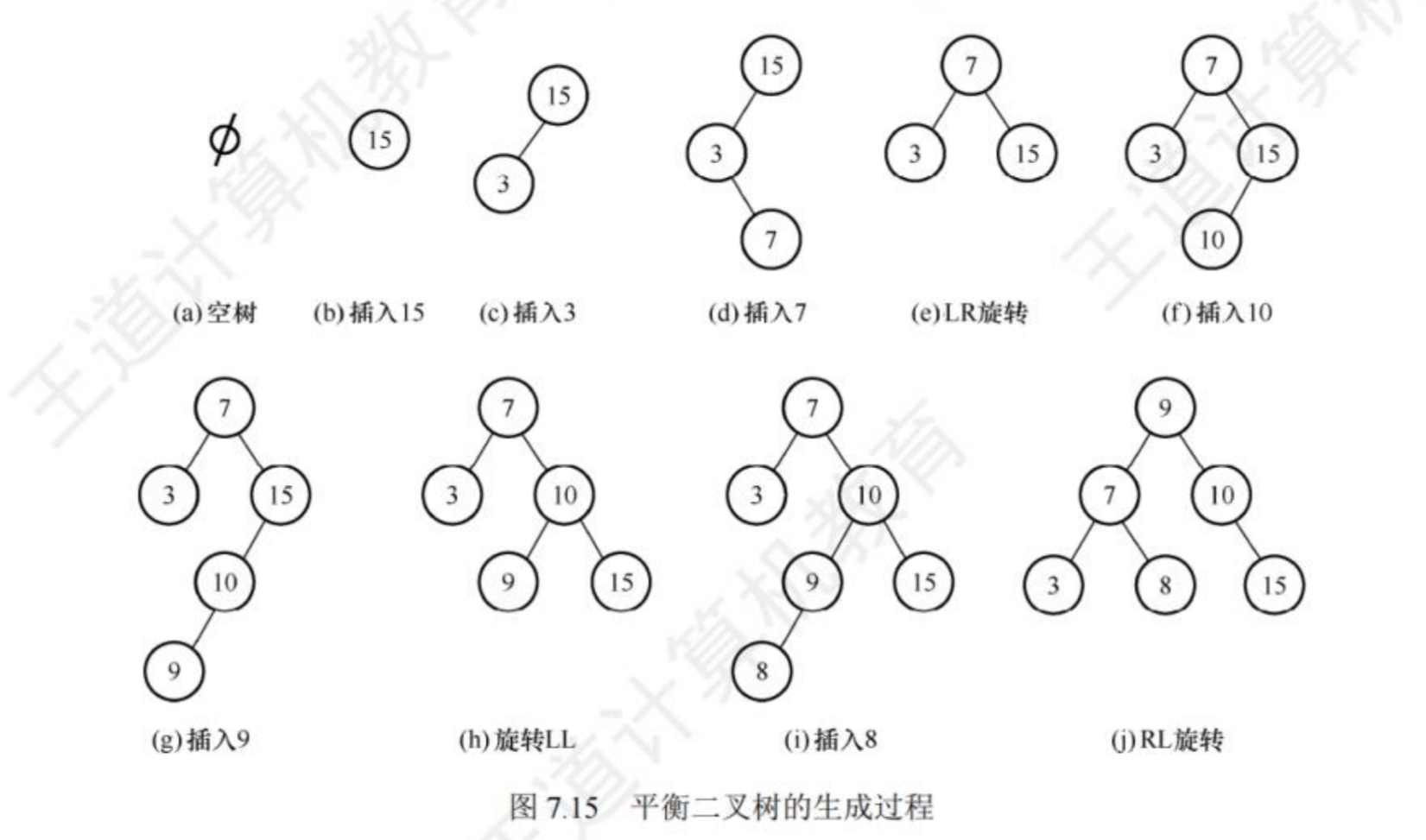
红黑树
我们知道AVL树是为了优化二叉排序树的查找而衍生出来的一种特殊的二叉排序树,但是AVL树对于平衡性的要求过于严格,导致其在插入和删除操作中需要频繁的调整整棵树的结构,导致其在构建的效率十分的低下,因此有没有一种构建过程不会特别复杂,不需要频繁的调整,而且查找起来的效率又会相对较高的结构呢?这就是这一节的主角:红黑树
定义及条件
红黑树是在AVL树的平衡标准上进一步的放宽条件所产生的一种特殊的二叉排序树结构。其最特殊的便是它的性质,红黑树的性质包括:
① 每个节点都是红色,或是黑色的。
② 根节点是黑色的。
③ 叶节点都是黑色的(***注意!此处的叶节点并非是指传统树形结构中没有左右孩子的那个节点*。而是在该(传统结构中的)叶子节点下,新构造的一种 虚拟 的,值为 NULL 的 外部节点)
④ 不存在两个相邻的红节点(即红节点的父节点和孩子节点均为黑色)
⑤ 对于每个节点,从该节点到任意一个叶子节点的简单路径(最短路径)上,所含的黑节点的数量相同。
外部节点:关于外部节点的定义在各百科及书籍中并没有给出统一的答案。不过在学习红黑树以及B树的时候,对外部节点的定义可以理解为是:在原本的叶节点中延伸出的一种并非实体的,值为NULL的一个特殊的全新的叶节点。因此在红黑树中,每一个叶节点(值并非为NULL的那一个叶节点)都会有两个(左右孩子各一个)不存在的外部节点。目的是为了保证红黑树中每一个节点的左右孩子均不为空。以下为一颗红黑树示例:
简单路径:在路径所经过的节点序列中,不存在重复经过的节点
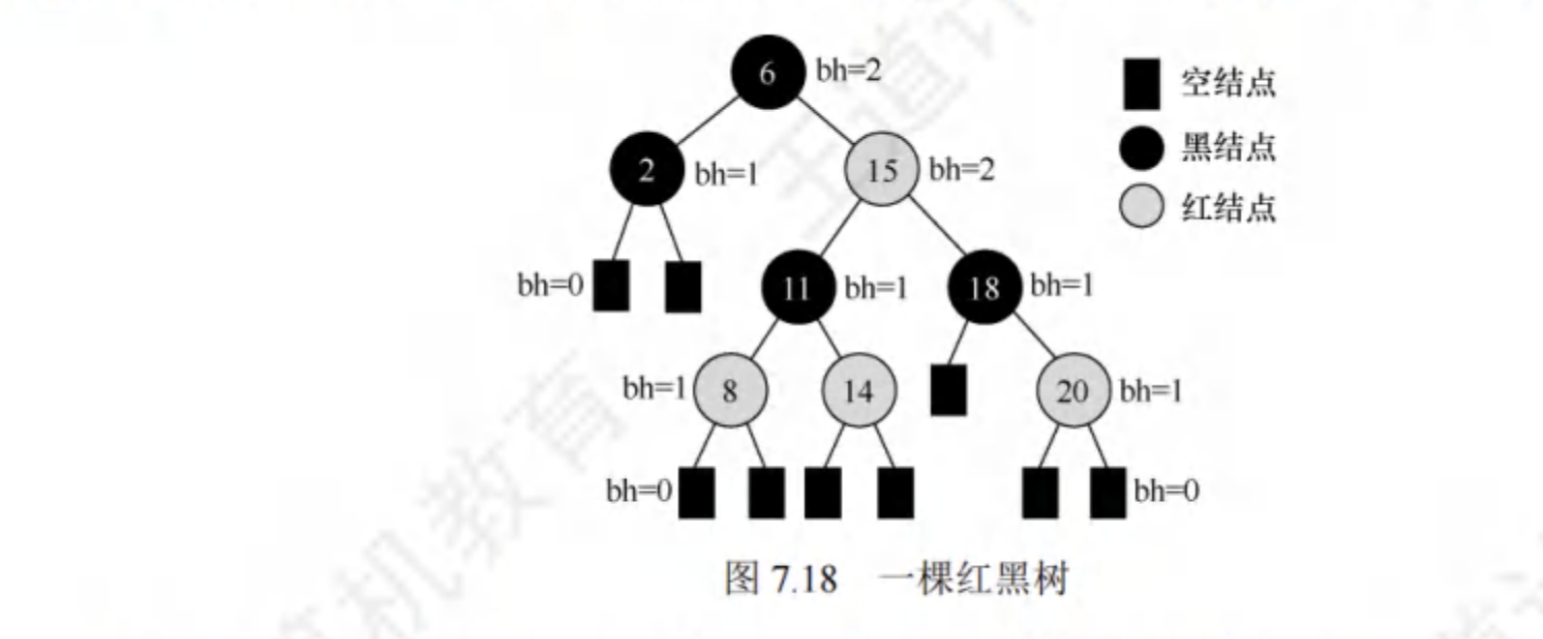
黑高(black high/bh):从某个节点出发(不包含该节点)到达一个叶节点(这里指的是值为NULL的外部节点)的任意一个简单路径上所经过的黑节点的个数。
你可以发现一件很神奇的事情:根节点6到任意一个叶节点,无论这个叶节点位于哪一层,其路径上所经过的黑节点的个数都是2!即bh=2。其他任意一个节点也是如此,只要他们是从相同的节点出发,到达任意一个叶节点所经过的黑色节点的总数都是一样的,此处对应的便是性质⑤。
相较于AVL树的高度平衡,红黑树的平衡条件由”左右子树高度差的绝对值不超过1”变为了左右子树的高度差不超过两倍”,由此便可以减少增删时的操纵频率。但查找性能相比AVL树会略微低些(因为影响查找效率的树高相比于AVL树还是稍微高了些),因此实际应用中如果是增删操作较少,查找操作为主的话采用AVL树最为合适。但其实红黑树的应用会更为广泛,如C++中的map和set就是用红黑树实现的。
红黑树的插入
红黑树的插入和二叉排序树的插入基本类似,不同之处在于,红黑树的插入需要对新插入的节点进行节点染色,以及对染色后的二叉树进行调整以符合红黑树的性质的操作。
新插入的节点初始为红色,此时便会面临以下几种情况:(设新插入节点为z)
① 若z的父节点为黑色,无需调整,这便是一颗标准的红黑树
② 若z为根节点,则将z染为黑色
③ 若z的父节点为红色,则此时看z的叔节点(z的父节点的兄弟节点):
1) z的叔节点是黑色的,z的父节点是(z的父节点的父节点的)左(L)孩子,且z是(z的父节点的)右(R)孩子,则属于LR,需要先左旋后右旋,z先左上旋转和其父节点交换位置,随后又右上旋转到其(原)父节点的父节点(或者说爷节点)的位置。使得z原本的父节点成为z的左孩子,z原本的爷节点成为z的右孩子。
2) z的叔节点是黑色的,z的父节点是左(L)孩子,
且z是左(L)孩子,则为LL,需要进行两次右旋,先是交换z和父节点的位置,后z再和(原)爷节点交换位置,爷节点成为z的右孩子。并且交换z(原)父节点和z(原)爷节点的颜色,使其符合红黑树的性质。
若z的父节点是右孩子,则还有RL(右旋再左旋)和RR(左单旋)两种情况,则与上面的操作类似,便不再赘述。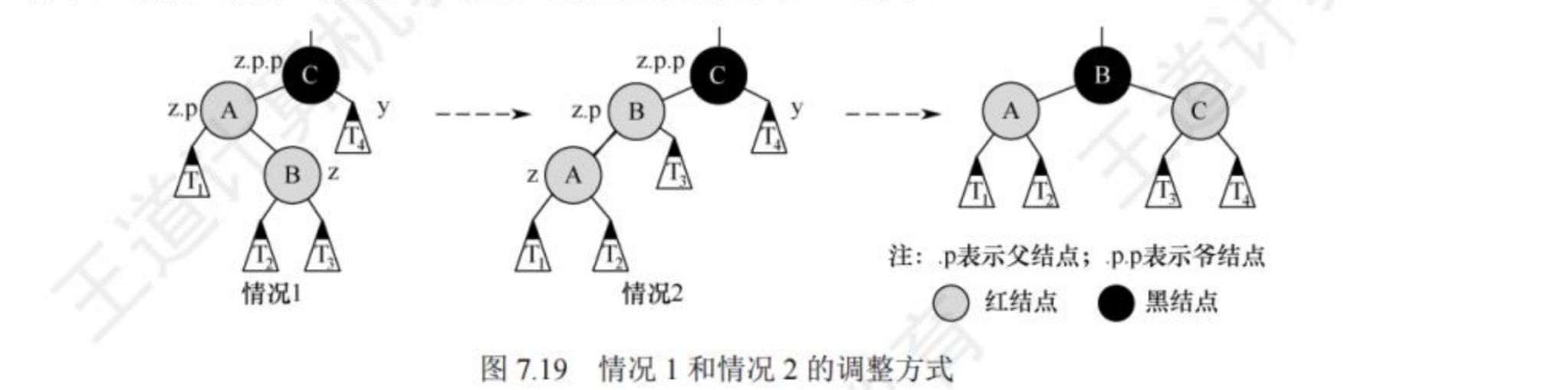
3) z的叔节点是红色的,此时z无论是左孩子还是右孩子都不影响了。因为爷节点是黑色的,所以要将父节点和叔节点都染为黑色,并将爷节点着为红色,以保持局部性质④和⑤。然后把爷节点作为新节点z重复循环,对爷节点的叔节点和父节点以及爷节点进行调整,直至调整完毕。
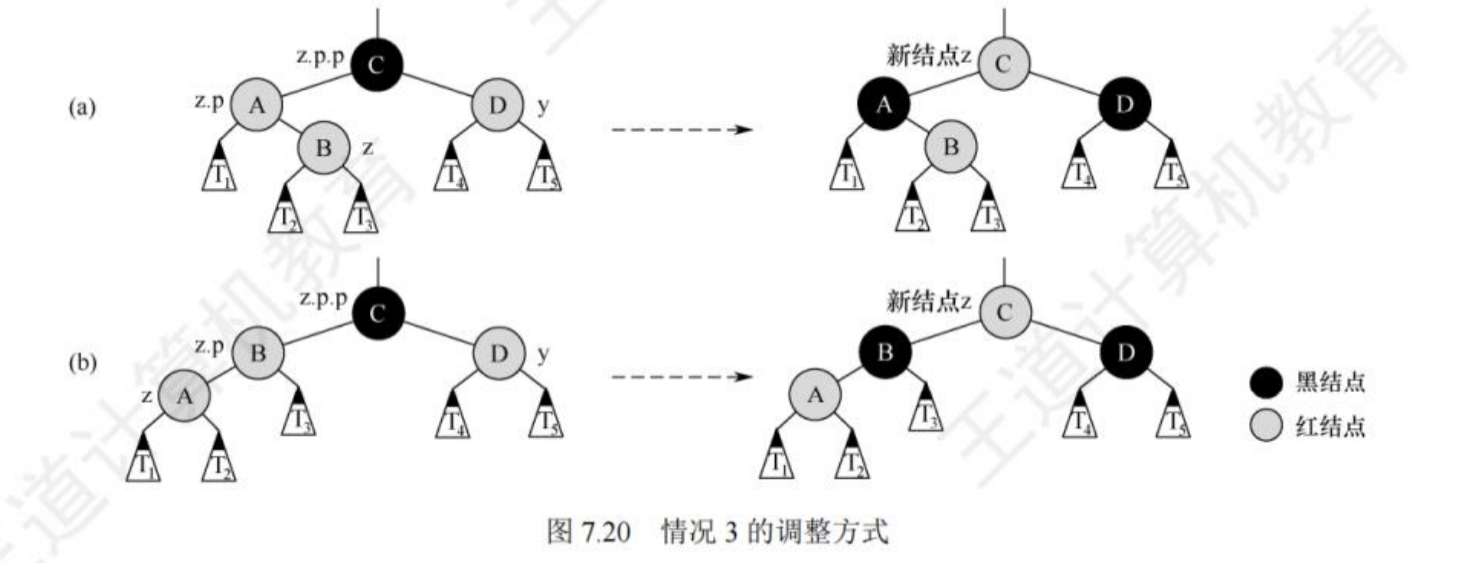
下面是一个红黑树插入的案例(虚线表示插入后未调整的状态):
插入节点5: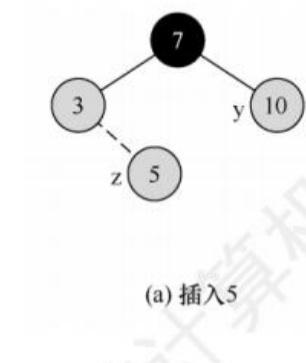
节点5和其父节点3均为红色,并且5的叔节10也为红色,此时为情况③中的3),需要将父节点和叔节点着为黑色,并将爷节点着色为红色。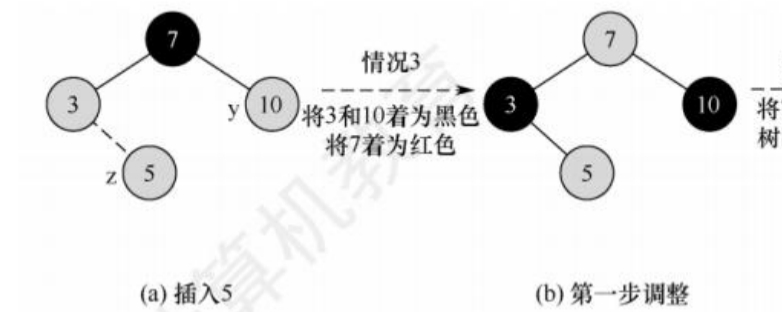
由于爷节点7为根节点,根据性质②,需要将根节点7染为黑色。此时调整结束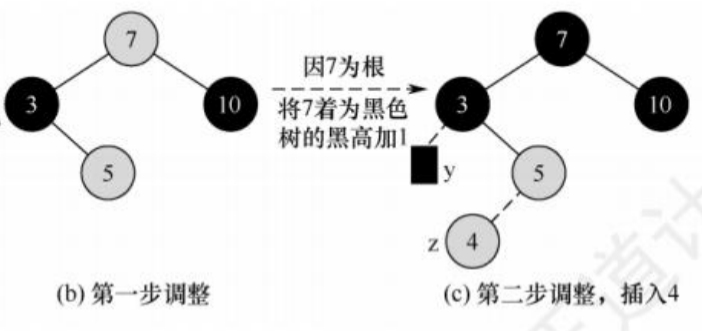
插入节点4,由于其父节点为红色,且叔节点(3的外部节点,外部节点默认黑色)为黑色,而4又是5的左孩子,因此是情况③中的1),也就是RL,那么此时需要先右旋再左旋,将4上升到原爷节点的位置。在上升的途中,4右旋至原父节点5的位置后,此时4和5均为红色,为情况③.2)的RR,因此需要交换3和4的颜色,再对3进行左旋,最后结束调整。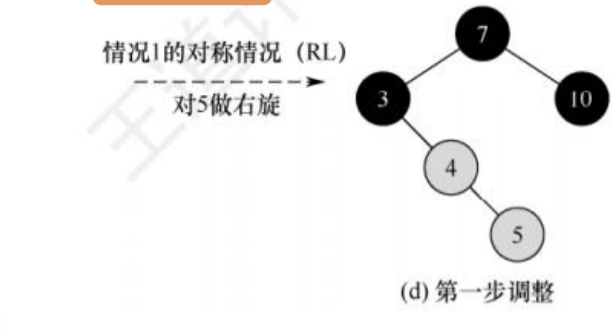
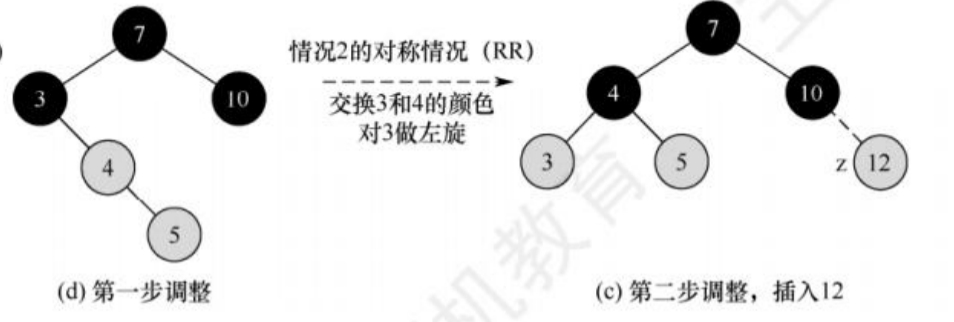
插入12,由于其父节点为黑色,无需任何调整,结束。
B树
定义及特性
B树是一种平衡因子均为0的绝对平衡树,也就是说是它对于平衡性的严格程度更甚于AVL树。
我们一般说一颗B树,都是称其为m阶B树,这里的m指的是一个节点最多可以有m个子树(因此B树不一定是二叉树)。而且较为特殊的是,B树中的一个节点可以有多个关键字。
下面是一颗5阶B树的示例: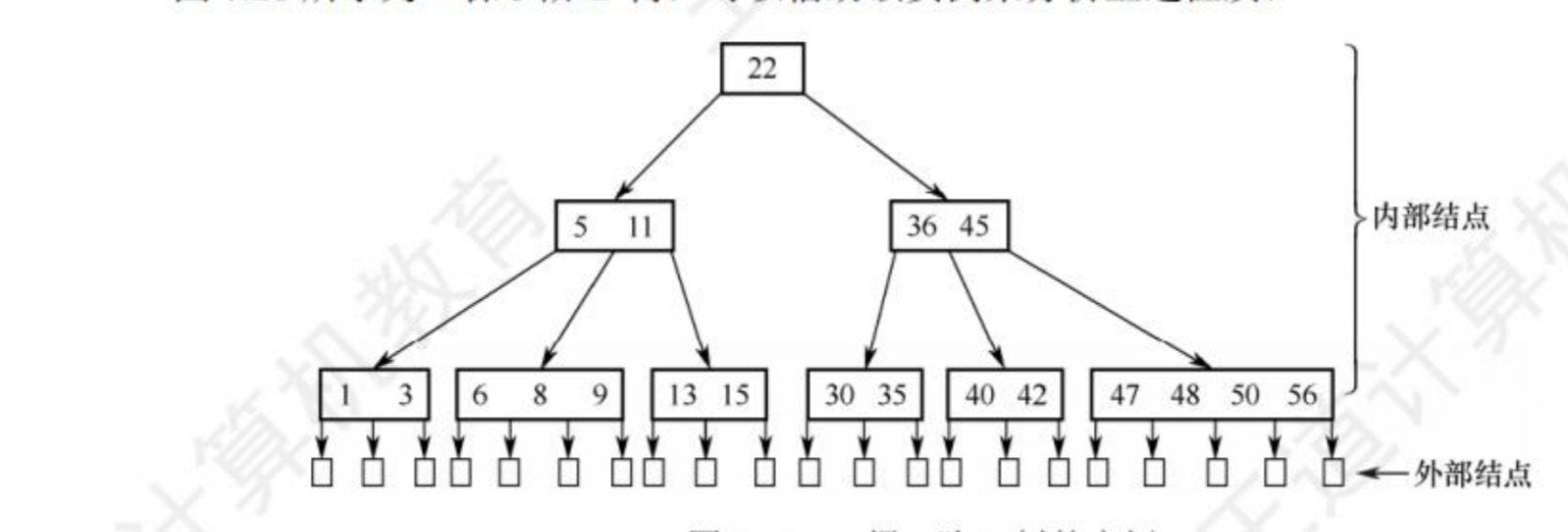
一颗m阶子树必须满足以下特性:
① 每个节点至多只能有m个子树,并且最多只能包含m-1个关键字。
② 若根节点不是叶节点,那么根节点至少有两颗子树,即至少有一个关键字。
③ 所有非根节点都至少有[m/2]颗子树,即至少有[m/2]-1个关键字。若m为奇数则向上取整,比如上面的示例中每个非根节点至少有[5/2]=3颗子树
④ 所有非叶节点的结构为:| p | K1 | p | K2 |….其中p为指向孩子节点的指针,K为当前节点内的元素。
⑤ 所有的叶节点都在同一层(理所应当的,因为B树是一颗绝对平衡的树),并且都是外部节点(不带信息),实际上这些外部节点并不存在,指向这些节点的指针为空。
注意!在实际应用中有的人习惯将叶节点视为内部节点中最底层的节点(即因指针指向为空查找失败的节点,也称作失败节点),而有的人会将叶节点定义为外部节点(也成为终端节点)
⑥ 节点中的关键字是有序的,并且父节点和子节点之间也是有序的。(例如示例中的节点5,1均小于父节点22,节点6,8,9均大于节点5,11中的5并均小于11,因此其箭头从5和11的中间位置出发。)
B树的结构有点像是区间的概念,子节点中的值均位于父节点中某两个值的区间内(所以箭头也是从两个树中间延伸出来),或者是均大于或小于某个边界值。在示例中:节点中一个元素的左指针所指的节点均小于该元素的值,右指针所指的节点均大于该元素的值。
因此B树也是一种特殊的排序树,满足左<中<右的特性。
B树的查找
B树的查找和二叉排序树很相似,不同的是B树每个节点都包含了可能不止一个的关键字,并且每个节点不只有两个分支,也可能会有多个分支。
B树的查找包含两个基本操作:①在B树中寻找节点;②在节点中寻找关键字或是关键字所处的区间。
B树查找的基本逻辑是:查找该节点中的有序表,若有查找到相应的元素则查找成功,若是没找到则根据其值在该节点所在的区间内(即指针所指的节点)进行查找。
例如,在上面的例子中,我们要查找关键字42,首先从根节点开始,44>22,因此若是存在44的话,一定是位于节点22的右子树中,因此查找右子树,右子树中有三个关键字,而36<42<45,若是节点44存在的话则是位于36和45的区间内,即36和45之间指针所指的节点内,因此查找其指针所指节点,在该节点中查找到关键字42,因此查找成功。若是查找到叶节点(外部节点,指针为空),则为查找失败,没有对应的关键字。
B树的插入
B树的插入类似于二叉排序树的插入,但是需要注意的是,一颗m阶B树中的所有节点最多包含m-1个关键字,而插入新的关键字可能会导致该节点的关键字数量溢出,因此当节点插入新的关键字时,需要检查插入后的状态是否符合B树对于节点关键字数量的性质,若是破坏了该性质则需要进行调整。
定位
在B树中插入新元素首先要做的是找到相对应的节点。根据B树的性质找到关键字所处的区间,并逐层的往下缩小区间(因此新元素的插入都是位于B树最底层的非叶节点),直至找到最小区间,或是查找失败(指向外部节点)。
插入
找到对应的位置后便可在该节点处进行插入,插入后还需对节点内部元素进行一次排序(一般排序的算法是选择排序或是直接排序)。若是插入的数据导致节点内部元素数量溢出的,就需要对节点元素进行优化。
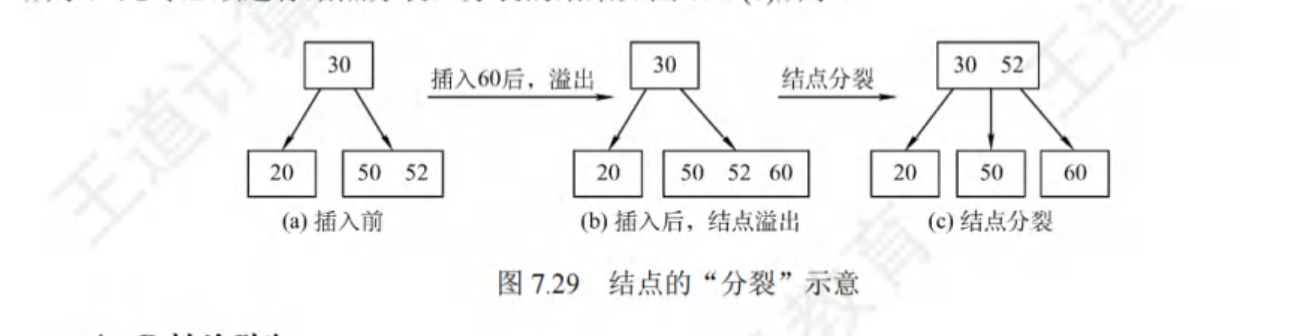
分裂
若该节点内部元素数量大于m-1,则需要对该节点进行分裂处理。
首先将该节点(假设有m个元素)中的第[m/2]个元素右边的所有元素放入一个新节点A中
再将第[m/2]个元素移至其父节点中。并将其右区间指向新节点A。
若是移动至父节点后导致其父节点的元素数量溢出,则重复上述步骤。
B树的删除
B树的删除和插入类似,也需要经历定位、修改、调整的操作。在删除某个节点后,若其节点中元素的数量小于[m/2]-1,即不满足B树的性质,则需要进行合并的操作.
定位
与插入相同,不再赘述。
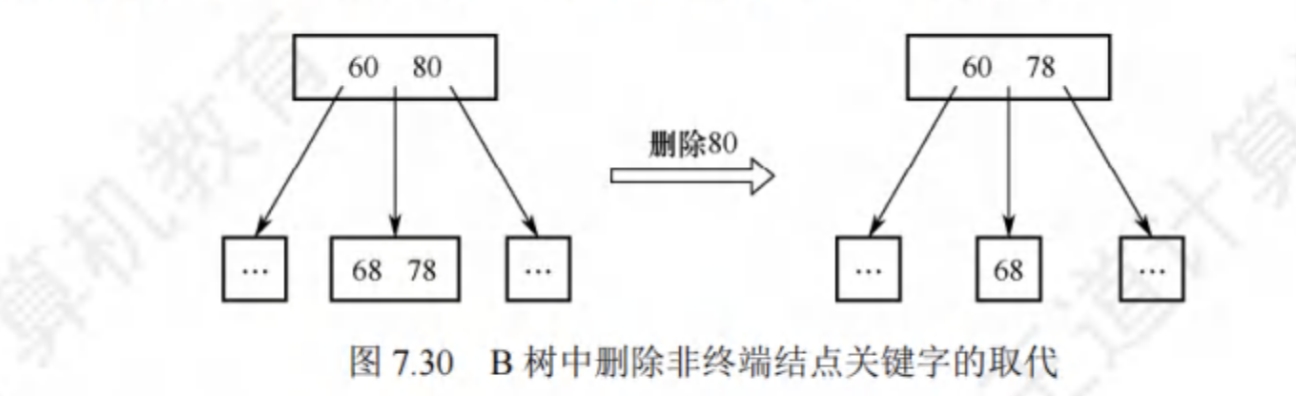
删除节点
节点的删除右三种情况:
① 直接删除关键字。若节点删除数据后元素的数量≥[m/2],则表明删除后仍符合B树定义,无需做出任何改变。
② 若删除数据后元素的节元素数量<[m/2]-1,则违反B树的性质。那么此时便需要向兄弟(左右都可)节点”借”一位关键字。
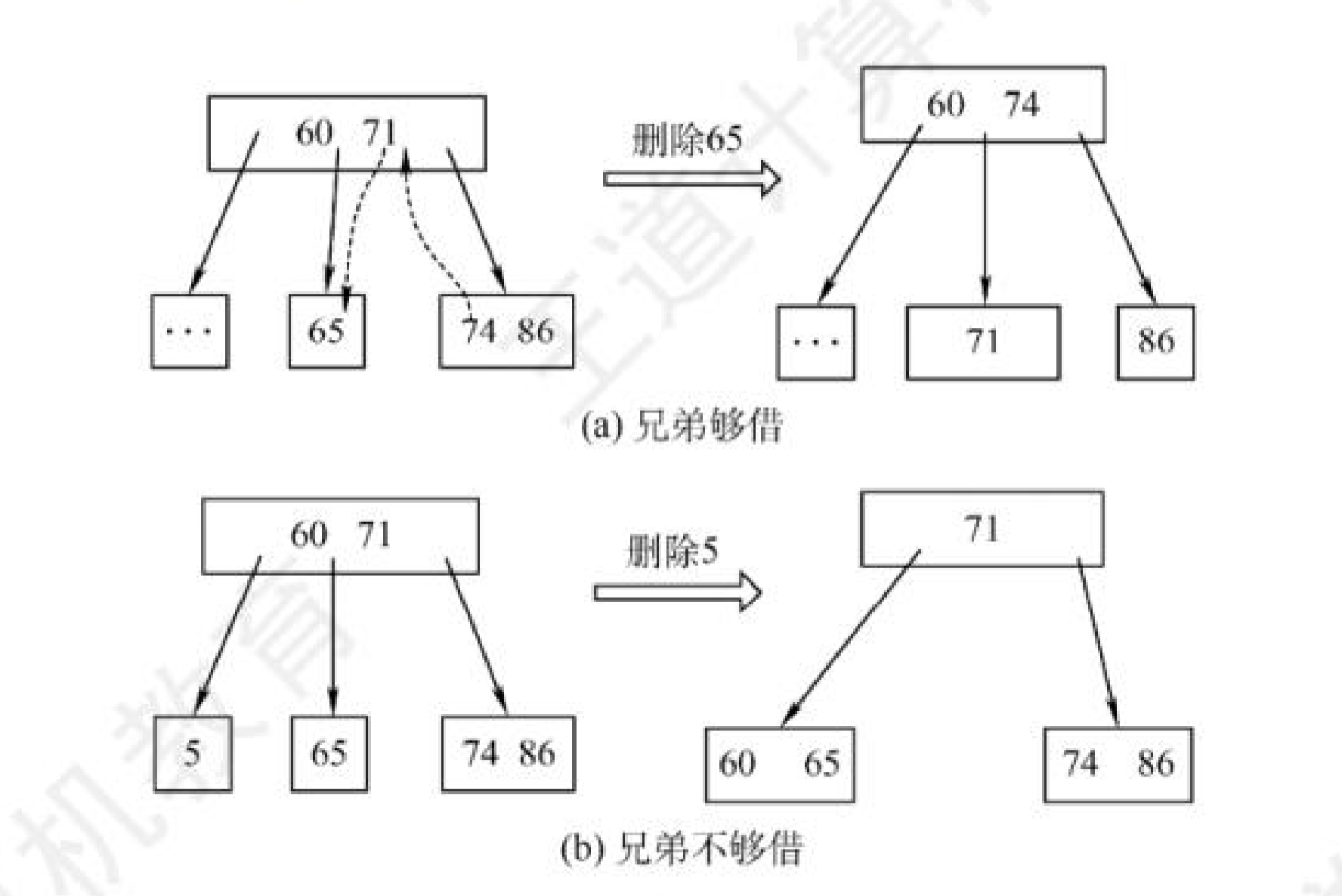
1) 若兄弟节点够借,即兄弟节点关键字个数≥[m/2],则借出节点后不会违反B树的性质。因此可以像兄弟节点借用一个关键字。从兄弟节点中借用一个最接近被删除节点的关键字A(左兄弟节点的话就是最右边的关键字,右兄弟节点的话就是最左边的关键字),将父节点中最接近被删除节点的元素移至被删除节点中,并将关键字A代替至父节点中移动的那个元素的位置。
2) 若兄弟节点不够借,即兄弟节点关键字个数=[m/2]-1,则借出节点的话会违反B树的性质,因此需要在关键字删除后与左(或右)兄弟节点以及双亲节点中的关键字进行合并。
(扩展)B+树
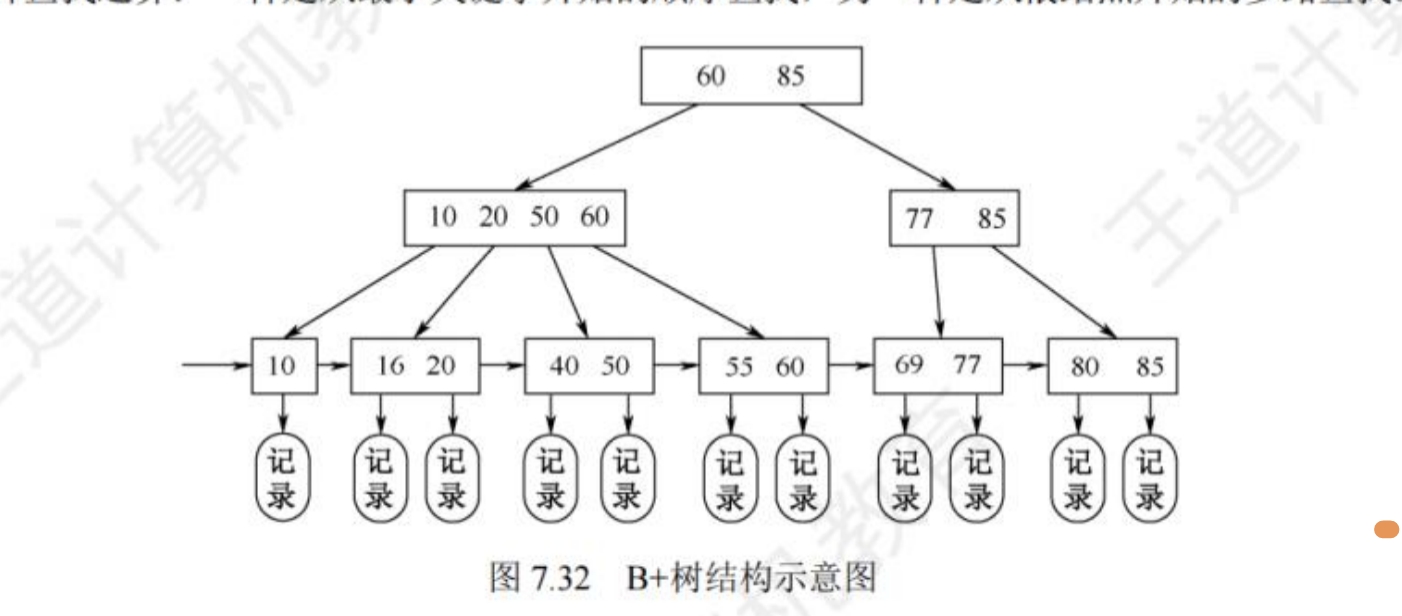
B+树多用于数据库的存储架构。与B树不同的是,从结构上来看,B树的子节点对应的是父节点中元素的区间,而B+树则对应的是父节点的元素。也就是说,B树一个有m个元素的节点最多可以有m+1个子树,而B+树的话m个元素的节点只有m个子树。
B+树的所有叶节点包含全部关键字(也就是说非叶节点的元素最终也会出现在叶节点上)以及指向相应记录的指针,叶节点中的关键字按大小顺序排序。
非叶节点仅起到索引作用,不含有对应记录的存储地址,这样可以使得一块磁盘能够存储更多的关键字,查找速度更快。